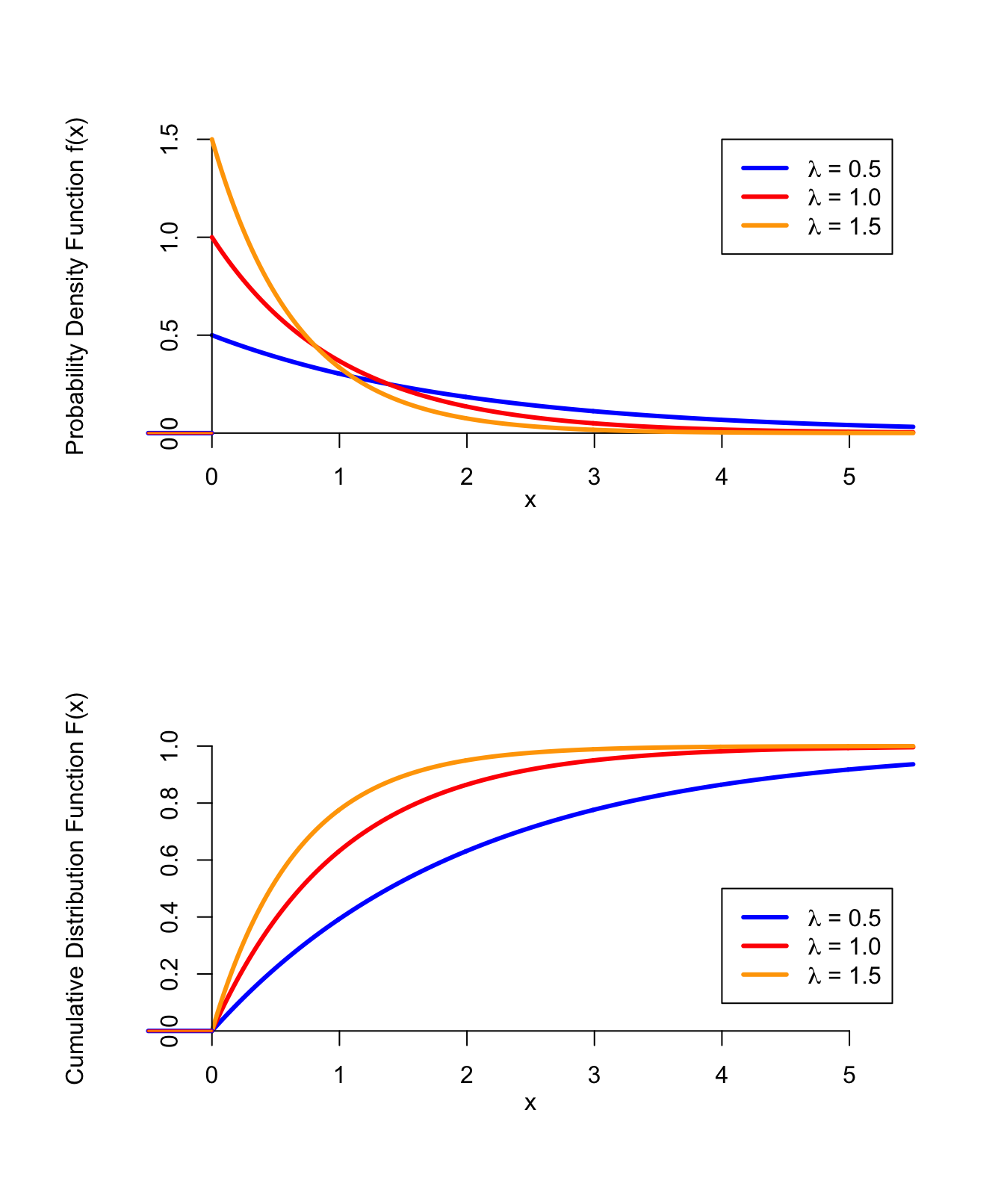
fertlessons.blogg.se - Exponential graph

#EXPONENTIAL GRAPH HOW TO#

We can decipher some information from the given graph itself, and we can then solve for other requirements for the exponential graph equation. Every graph will provide different information depending on its type. We can find the exponential function equation from a given graph.

#EXPONENTIAL GRAPH HOW TO#

How to Find Exponential Function from a Graph? While one end will reach a horizontal asymptote, the other will approach negative or positive infinity along the y-axis.

Step 3: We will extend the curve on both ends.

Step 2: Now, we will use the points to sketch a graph curve, establishing the direction of the slope and the y-intercept.

We will begin with x= -1, 0, 1, and find additional points if required.

Step 1: We will evaluate the exponential function for different values of x.

The following steps will help you graph exponential functions easily: Now, we can graph the exponential function. To graph exponential function, f (x) = 2 x+1, we will calculate a few more points This horizontal line that the exponential function graph approaches but fails to reach is called the horizontal asymptote. It approaches but does not reach the horizontal line. When we graph exponential functions, the value of y grows to positive or negative infinity towards one end. We study what happens to the value of y when x becomes very large in positive or negative directions. The term end-behavior refers to the relation between x and y.

When f (1) f(0), the slope of the graph is positive.

When f (1) > f (0), then the graph has a positive slope.

The following two statements will help you determine the slope of the exponential function graph. The slope is either increasing or decreasing. To determine the slope of the graph, we use f (0) and f (1). We have to evaluate the function at x = 0, to find the value of the y-intercept. The y-intercept of an exponential graph is important as it helps us identify a number of other features.

How does the value of y change with an increase in the value of x?.Whether the slope of the graph positive or negative?.Using the points on a graph, we can identify the following important features of the graph: So, we have our first point for the graph now, that is (1, 3). To find the value of y when x =1, we can use f(1) For instance, for the function f (x) = 2 x +1.

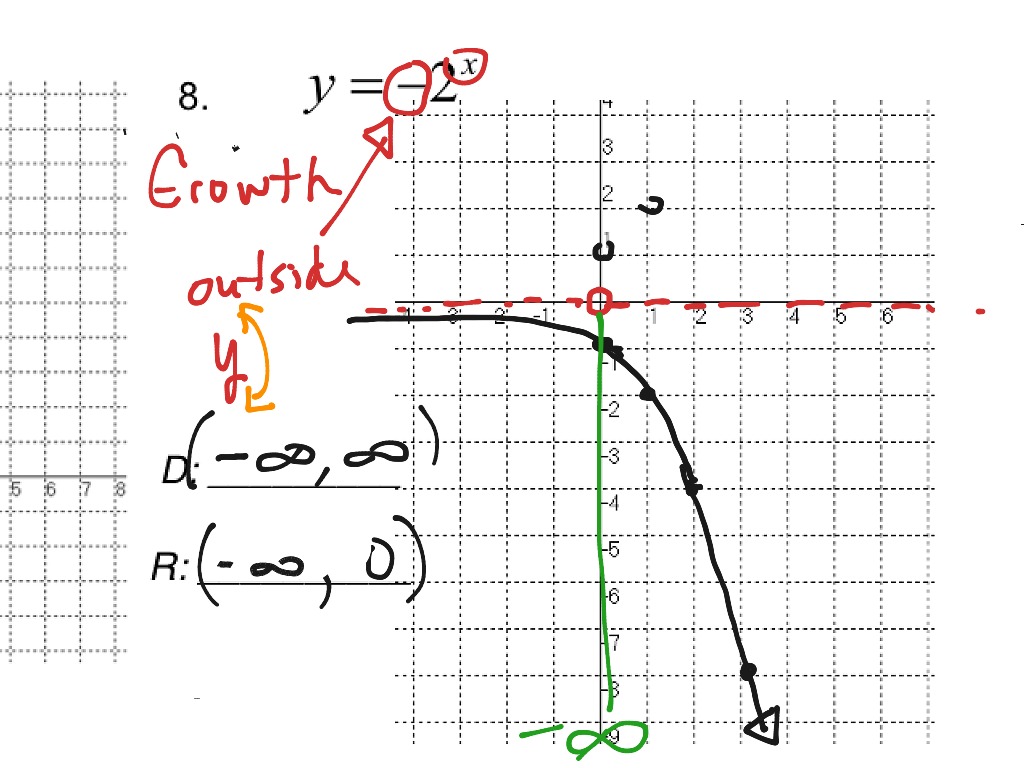
Now, calculate the output value from the input value. One of the best ways to graph exponential functions is by finding a few graph points and sketching the graph based on those points.įor finding a point on the graph, we will first select an input value. Now, we will learn how to graph exponential functions. Also, the curve will get steeper as the exponent increases. Here, x > 1, the value of y = fn(x) will increase when we increase the values of (n). This graph is always nonlinear as its slopes are always changing. Which graph represents an exponential function? An exponential function graph is an upward curve, as shown in the following image. Example 2: Solve 5 1-x = 5 5 Solution: Since the given bases are the same (i.e., 5), we will equate the powers. Example 1: Solve 4 x = 4 5 Solution: Since the given bases are the same (i.e., 4), we will equate the powers. Answer: The value of x is 5. Here a> 0 and b>0, x and y are real numbers. You must understand the properties of the exponential functions to perform calculations. So, the derivative of the exponential function is the function itself as given below:į ‘(x) = ex = f(x) Properties of Exponential Functions Also, the exponential function f(x) =e x has a special property.